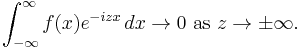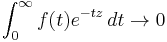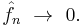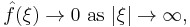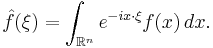Riemann–Lebesgue lemma
In mathematics, the Riemann–Lebesgue lemma, named after Bernhard Riemann and Henri Lebesgue, is of importance in harmonic analysis and asymptotic analysis.
The lemma says that the Fourier transform or Laplace transform of an L1 function vanishes at infinity.
Contents |
Statement
Let ƒ:R → C be a measurable function. If ƒ is L1 integrable, that is to say if the Lebesgue integral of |ƒ| is finite, then
This says that the Fourier transform of ƒ tends to 0 as z tends to infinity.
Other versions
The Riemann–Lebesgue lemma holds in a variety of other situations.
- If ƒ is L1 integrable and supported on (0, ∞), then the Riemann–Lebesgue lemma also holds for the Laplace transform of ƒ. That is,
-
- as |z| → ∞ within the half-plane Im(z) ≥ 0.
- A version holds for Fourier series as well: if ƒ is an integrable function on an interval, then the Fourier coefficients of ƒ tend to 0 as n → ±∞,
-
- This follows by extending ƒ by zero outside the interval, and then applying the version of the lemma on the entire real line.
- The lemma also holds for the Fourier transform in higher dimensions. If ƒ ∈ L1(Rn), then
-
- where
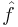 is the Fourier transform
is the Fourier transform
Applications
The Riemann–Lebesgue lemma can be used to prove the validity of asymptotic approximations for integrals. Rigorous treatments of the method of steepest descent and the method of stationary phase, amongst others, are based on the Riemann–Lebesgue lemma.
Proof
The proof of the last special case can be organized into 3 steps; the 4th step extends the result to the first special case.
Step 1. An elementary calculation shows that
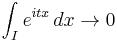 as
as 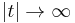
for every interval I ⊂ [a, b]. The proposition is therefore true for all step functions with support in [a, b] (similarly, the proposition is also true for a slightly larger class of functions known as simple function).
Step 2. By the dominated convergence theorem, the proposition is true for all positive functions, integrable on [a, b].
Step 3. Let f be an arbitrary measurable function, integrable on [a, b]. The proposition is true for such a general f, because one can always write f = g − h where g and h are positive functions, integrable on [a, b].
Step 4. Because functions with compact support are dense in L1(R), this special case extends to the general result if we require t to be real.
The case of non-real t. Assume first that f has a compact support on 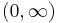 and that f is continuously differentiable. Denote the Fourier/Laplace transforms of f and
and that f is continuously differentiable. Denote the Fourier/Laplace transforms of f and 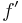 by F and G, respectively. Then
by F and G, respectively. Then 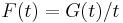 , hence
, hence 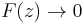 as
as 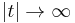 . Because the functions of this form are dense in
. Because the functions of this form are dense in 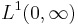 , the same holds for every f.
, the same holds for every f.
References
- Bochner S., Chandrasekharan K. (1949). Fourier Transforms. Princeton University Press.
- Weisstein, Eric W., "Riemann–Lebesgue Lemma" from MathWorld.